XOR 加密简介

本文介绍一种简单高效、非常安全的加密方法：XOR 加密。

一、 XOR 运算

逻辑运算之中，除了 AND 和 OR，还有一种 XOR 运算，中文称为"异或运算"。

它的定义是：两个值相同时，返回false，否则返回true。也就是说，XOR可以用来判断两个值是否不同。

true XOR true // false
false XOR false // false
true XOR false // true
true XOR false // true

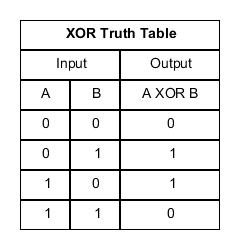
JavaScript 语言的二进制运算，有一个专门的 XOR 运算符，写作^。

1 ^ 1 // 0
0 ^ 0 // 0
1 ^ 0 // 1
0 ^ 1 // 1

上面代码中，如果两个二进制位相同，就返回0，表示false；否则返回1，表示true。

二、 XOR 的应用

XOR 运算有一个很奇妙的特点：如果对一个值连续做两次 XOR，会返回这个值本身。

// 第一次 XOR
1010 ^ 1111 // 0101

// 第二次 XOR
0101 ^ 1111 // 1010

上面代码中，原始值是1010，再任意选择一个值（上例是1111），做两次 XOR，最后总是会得到原始值1010。这在数学上是很容易证明的。

三、加密应用

XOR 的这个特点，使得它可以用于信息的加密。

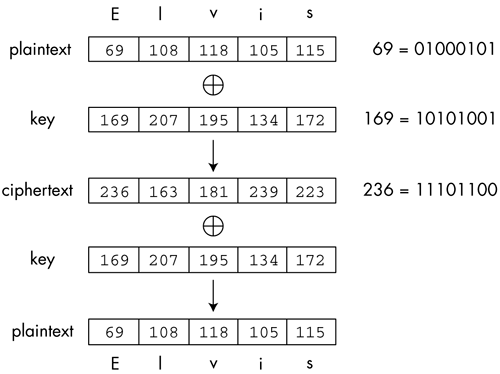
message XOR key // cipherText
cipherText XOR key // message

上面代码中，原始信息是message，密钥是key，第一次 XOR 会得到加密文本cipherText。对方拿到以后，再用key做一次 XOR 运算，就会还原得到message。

四、完美保密性

二战期间，各国为了电报加密，对密码学进行了大量的研究和实践，其中就包括 XOR 加密。

战后，美国数学家香农（Claude Shannon）将他的研究成果公开发表，证明了只要满足两个条件，XOR 加密是无法破解的。

• key的长度大于等于message
• key必须是一次性的，且每次都要随机产生

理由很简单，如果每次的key都是随机的，那么产生的CipherText具有所有可能的值，而且是均匀分布，无法从CipherText看出message的任何特征。也就是说，它具有最大的"信息熵"，因此完全不可能破解。这被称为 XOR 的"完美保密性"（perfect secrecy）。

满足上面两个条件的key，叫做 one-time pad（缩写为OTP），意思是"一次性密码本"，因为以前这样的key都是印刷成密码本，每次使用的时候，必须从其中挑选key。

五、实例：哈希加密

下面的例子使用 XOR，对用户的登陆密码进行加密。实际运行效果看这里。

第一步，用户设置登陆密码的时候，算出这个密码的哈希，这里使用的是 MD5 算法，也可以采用其他哈希算法。

const message = md5(password);

第二步，生成一个随机的 key。

// 生成一个随机整数，范围是 [min, max]
function getRandomInt(min, max) {
  return Math.floor(Math.random() * (max - min + 1)) + min;
}

// 生成一个随机的十六进制的值，在 0 ～ f 之间 
function getHex() {
  let n = 0;
  for (let i = 4; i > 0; i--) {
    n = (getRandomInt(0, 1) << (i - 1)) + n;
  }
  return n.toString(16);
}

// 生成一个32位的十六进制值，用作一次性 Key
function getOTP() {
  const arr = [];
  for (let i = 0; i < 32; i++) {
    arr.push(getHex());
  }
  return arr.join('');
}

上面代码中，生成的key是32位的十六进制值，对应 MD5 产生的128位的二进制哈希。

第三步，进行 XOR 运算，求出加密后的message。

function getXOR(message, key) {
  const arr = [];
  for (let i = 0; i < 32; i++) {
    const  m = parseInt(message.substr(i, 1), 16);
    const k = parseInt(key.substr(i, 1), 16);
    arr.push((m ^ k).toString(16));
  }
  return arr.join('');
}

使用这种方法保存用户的登陆密码，即使加密文本泄露，只要一次性的密钥（key）没有泄露，对方也无法破解。

（完）